1) A⇒¬B
2) Aが真ならBは未定義(三値論理の利用)
3) Aの真偽による場合分け
の三通りが考えられる。
1)の場合REQ制約の否定として表現できる。CEGTestの場合は、
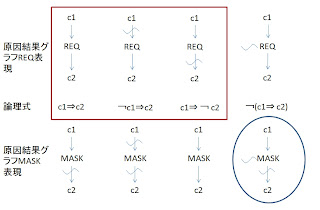
青丸で囲んだところはちょっと怪しい。と言うか括弧で括るような、否定を取る優先順位を決めなければならない。そう言うことを考えなくても良いようにREQとMASKが定義してあると言うのは合理的かも知れない。ただし、最近FXの秋山氏の指摘で新たな謎が生まれた。MASKは結果側に付ける[1]と言うものである。もしそうなら原因結果グラフは結構簡単で使いやすいものになる気がする。この謎の裏にどんな合理性があるのか調べてみたい。
2)調べてみると三値論理には何種類もある[2]。マスクされた側をどう解釈するか(a.真か偽か決まらない状態、b.真でも偽でもない第三の状態、c.無意味)によって使用する論理系が変わる。VDMはaによって未定義を扱える。ただし、実装上の都合で一部変更して利用している[3]。用途によって結構自由に使って良い見たいな感じである。原因結果グラフを命題論理の範囲で扱うことを考えているので、各ノードは命題でなければならず、単に真偽が決まっていない状態とするのが話が難しくならなくて良いと思う。VDMの様な手直しをするかどうかはまた別の問題として考えれば良いだろう。三値論理を使うと、結果側に不定が現れる。結果側に現れる不定が妥当かどうか、ちゃんと解釈できるかどうかで使用する論理系を決めれば良いと思う。それで、幾つかやってみたが三値論理を使わなかった場合すなわち、1)の方法で真にも偽にもなり得るという結果に落ち着く。aの場合の真理表は以下のようになる。*が真偽が決まらない状態。赤いところをVDMでは*として扱う。
| A | B | A∧B | A∨B | A⇒B | ¬A |
|---|---|---|---|---|---|
| T | T | T | T | T | F |
| T | F | F | T | F | |
| T | * | * | T | * | |
| F | T | F | T | T | T |
| F | F | F | F | T | |
| F | * | F | * | T | |
| * | T | * | T | T | * |
| * | F | F | * | * | |
| * | * | * | * | * |
3)“A masks B”をAが真の時はBを考慮しなくて良いというそのままの意味に解釈して。Aが真の時はBを含まない原因結果グラフを作ってしまう。これは、原因結果グラフ全体を表す論理式の真偽がどのような意味を持つのかに関わる問題と関係する。
参考文献
[1] http://en.wikipedia.org/wiki/Cause-effect_graph
[2]http://ja.wikipedia.org/wiki/3値論理
.jpg)



.jpg)




